시계열 데이터 분해를 통한 예측

현재 재직 중인 회사(이 글은 2021년 11월에 작성되었음)는 상당한 트랜잭션이 발생되고 있고, 따라서 트래픽의 양에 따라 서버를 scaling하는 작업이 중요하다. 트래픽이 적을 때는 서버 규모를 축소하고, 많을 때만 잠깐 확장하는 것은 비용 효율적으로 서버를 운영하는 데 있어서 중요하다.

 

서버 개발자가 오토 스케일링에 관심을 가지게 되면 초기에는 단순한 조건 충족에 따른 스케일링이 되는데(cold starting), 거기서 더 발전하면 트래픽량을 예측하여 warm starting을 할 수 있다. 따라서 트래픽량이 중요한 기업들은 트래픽량을 예측하는 데에 관심이 많다.

 

데이터 사이언스 분야에서는 트래픽 예측 태스크를 Time Series Forecasting 문제의 한 축으로 보고 많은 연구를 진행 중이다. RNN, Transformer, TCN 등의 모델이 주로 활용되고 있다.

 

다만 시계열 데이터가 뚜렷한 주기성을 가지고 있으며, 예상치 못하는 peak가 적을 경우 딥러닝까지 가지도 않고 정말 간단한 코드로도 어느 정도 준수한 예측을 진행할 수 있다.

 

본 포스팅에서는 CloudWatch로부터 트래픽 Metric을 뽑아 단변량 지표만으로 어느 정도의 예측을 뽑아내는 간단한 모듈을 개발하는 과정에 대해 적어보려 한다.

다루기 쉬운 데이터(비정기적인 peak의 발생이 적고 주기성이 뚜렷한 데이터)일 때만 적용 가능하며, 어려운 데이터의 경우 시계열 데이터 분해에 대한 심도 있는 고민이 필요할 것이다.

데이터 추출 - CloudWatch

AWS CloudWatch에서는 지표(Metric)이라는 데이터를 제공한다. 나는 AWS Elastic Load Balancer에서 발생하는 RequestCount(요청 수)를 활용했는데, 이 경우 다음과 같이 코드를 작성할 수 있다.

from datetime import datetime, timedelta
import boto3
import numpy as np

def query_cloudwatch():
    client = boto3.client('cloudwatch')
    data = client.get_metric_data(
        MetricDataQueries=[
            {
                'Id': '메트릭 ID. 아무거나 적어도 된다.',
                'MetricStat': {
                    'Metric': {
                        'Namespace': 'AWS/ApplicationELB',
                        'MetricName': 'RequestCount',
                        'Dimensions': [
                            {
                                'Name': 'LoadBalancer',
                                'Value': '로드 밸런서의 ID'
                            },
                        ]
                    },
                    'Period': 300, # 60의 배수를 적는다.
                    'Stat': 'Sum',
                },
                'ReturnData': True,
            },
        ],
        StartTime=datetime.now() - timedelta(days=63),
        EndTime=datetime.now(),
    )['MetricDataResults'][0]

    x = data['Timestamps'][::-1]
    y = data['Values'][::-1]

    return x, y

def load():
    x, y = query_cloudwatch()
    x = np.array([d.replace(tzinfo=None) + timedelta(hours=9) for d in x])
    y = np.array(y)
    return x, y

Period는 Metric에 대한 기간인데, 60으로 설정하고 Stat을 Sum(합계)로 설정하면 60초 동안 발생한 요청수의 합을 리턴하며 1분 단위의 데이터를 제공한다. 즉, StartDate와 EndDate가 한 시간 차이라면 리턴되는 데이터는 60개이다.

이에 관해 아래와 같이 작성해두면 추후에 편하다.

PERIOD = 300
assert PERIOD % 60 == 0 and 3600 % PERIOD == 0

MINUTE = 60 / PERIOD
HOUR = 3600 // PERIOD
DAY = HOUR * 24
WEEK = 7 * DAY

CloudWatch는 Period에 따라 로그 저장 기간이 다르므로 이에 유의하여 MetricDataQueries 파라미터를 넘겨주어야 한다.

TimeStamps와 Values를 역순으로 재정렬한 것은 정렬이 내림차순(최신에서 나중)이기 때문이다.

 

timezone 정보를 없애고 UTC에 9시간을 더해 KST로 변환해주었다. 이를 cloudwatch.py파일에 작성하면 이후 load() 함수만으로 쉽게 로드할 수 있다.

데이터 파악

이렇게 얻은 데이터를 pyplot으로 출력해보자.

import matplotlib.pyplot as plt
import cloudwatch

X, Y = cloudwatch.load()
plt.plot(X, Y)
plt.show()

(그림은 난수로 생성한 가상의 데이터이다.

주기성 시계열 난수를 생성하려고 별 짓을 다 했다.... 어렵네..

)

주기성이 있는 것처럼 보인다. 간단하게 시계열 분해를 적용해보겠다.

시계열 데이터 주기성 분해

from statsmodels.tsa.seasonal import seasonal_decompose

res = seasonal_decompose(Y, period=DAY)
res.plot()
plt.show()

seasonal 항목을 보면 일 단위의 주기성을 캐치한 걸 볼 수 있다. residual 항목에서도 언뜻 주기성이 보이는 듯하다. 실제로 아래와 같이 확인해보면 잔차에도 주기성이 존재하는 것을 알 수 있다.

res = seasonal_decompose(Y, period=DAY)
res = seasonal_decompose(res.resid[~np.isnan(res.resid)], period=DAY)
res.plot()
plt.show()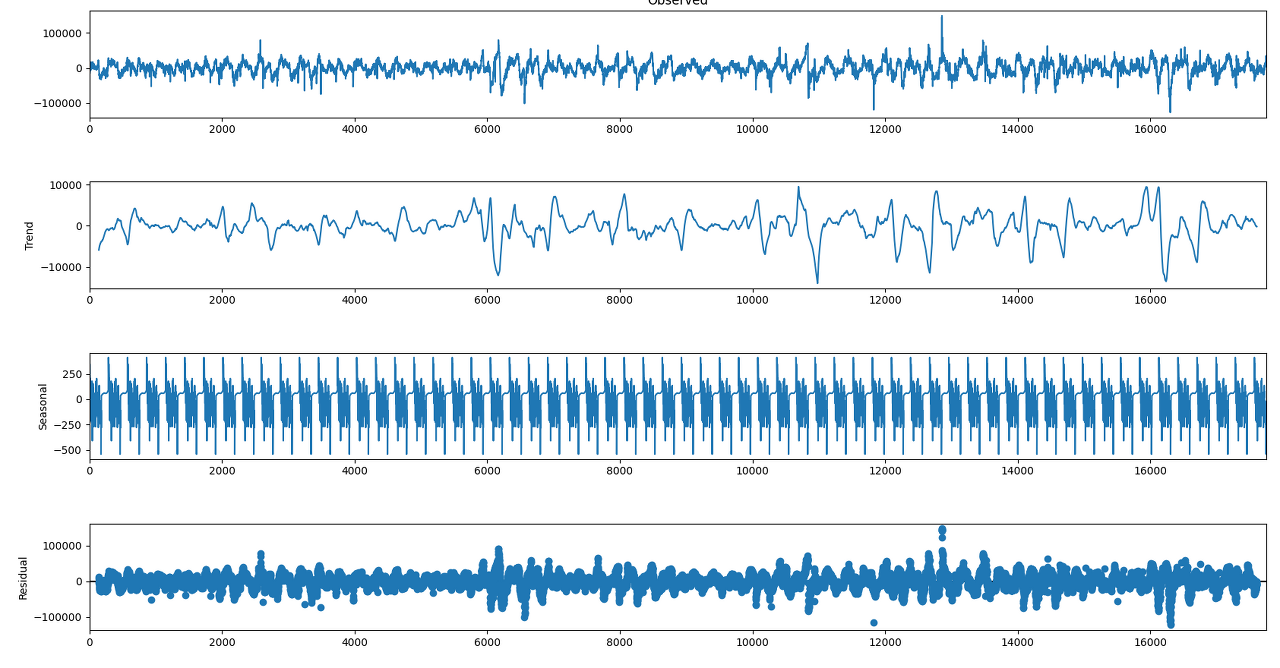

물론 처음 분석된 것에 비하면 적은 수준의 주기성이지만, 마냥 무시하기도 어려운 수준이다.

한 번 더 분해를 했음에도 잔차에 주기성을 보이는 게 여기서 활용하는 statsmodels에서 제공하는 분해 모듈의 한계인 듯하다.

"어떻게 더 세밀한 분해를 할 수 있을까?" 고민하는 것도 방법이지만, 사실 그냥 무지성으로 분해를 반복하는 것도 좋은 방법이 될 수 있다.

def get_seasonal_pattern(series):
    # return multiplicative seasonal pattern
    periods = [WEEK] * 5 + [DAY] * 5 + [WEEK] * 5
    seasonal_patterns = []

    input_ts = series
    for p in periods:
        res = seasonal_decompose(series, model=model, period=period)
        s = res.seasonal[~np.isnan(res.seasonal)]
        # 분해시 양쪽에서 period만큼 짤리므로 추가로 붙여준다.
        # seasonal 데이터는 반복적인 데이터라 이런 식으로 해도 무방하다.
        s = np.concatenate([s[p // 2:p], s, s[-p:-p // 2]]) 
        seasonal_patterns.append(s)
        input_ts = input_ts / s

    seasonal_pattern = np.prod(seasonal_patterns, axis=0)

    return seasonal_pattern

위 코드는 주 단위로 5번, 일 단위로 5번, 다시 주 단위로 5번 분해한 코드이다. 이유는 없다. 정말 무지성으로 반복한 거다. 시계열 데이터를 열심히 공부하는 혹자는 내 이런 방식을 보고 열불이 뻗힐 수도 있겠다.

죄송하게도 필자는 시계열 데이터 도메인의 전문가가 아니다.

솔직히 15번이나 반복할 이유는 없다... 아마 5번만 해도 될 거다.

아무튼, 위와 같이 얻은 패턴을 월요일 0시 0분부터 금요일 23시 55분까지 데이터로 잘라내자.

timestamps, request_counts = cloudwatch.load()

# 최신 데이터는 불안정(집계가 덜 되는 등)할 수 있으므로 버림
timestamps = timestamps[:-1]
request_counts = request_counts[:-1]

# time series decomposition(multiplicative model)
seasonal_pattern = get_seasonal_pattern(request_counts)

offset = [i for i, d in enumerate(timestamps) if (d.hour + d.minute + d.second + d.weekday() == 0)][0]
weekly_pattern = seasonal_pattern[offset:offset + WEEK]

이제 weekly_pattern 어레이를 반복하여 trend 데이터에 곱해주면 된다.

weekly_pattern을 인덱싱하여 쉽게 활용할 수 있는 함수를 작성하자.

def expand_weekly_pattern(seasonal_pattern, timestamps):
    T = np.array([(t.weekday() * DAY + t.hour * HOUR + (t.minute * 60 // PERIOD)) for t in timestamps])
    return seasonal_pattern[T]

timestamps 파라미터에 datetime array로 특정 날짜들을 입력하면 그 날짜에 해당하는 seasonal pattern이 반환된다.

시계열 데이터의 경향성 데이터

seasonal pattern을 구했으니 trend를 구하자. 사실 현재 사용하고 있는 seasonal_decompose 함수에서 trend 데이터를 제공하는데, 전후로 PERIOD만큼 잘린다. 나는 이게 너무 불편해서 따로 trend 값을 구했다.

아래 코드는 seasonal_decompose 함수가 반환하는 trend 값과 정확히 동일한데, 양 끝의 데이터를 보충했다는 점에서 다르다.

# convolution 연산을 통해 moving average 데이터를 계산
# conv 연산은 시퀀스 양 끝이 잘리므로 길이를 늘렸다가 다시 자른다.
# 그 결과는 위 seasonal_decompose 결과와 동일. 다만 잘리지 않은 데이터를 구할 수 있음.
x = np.concatenate([
    np.array([request_counts[0]] * (DAY // 2)),
    request_counts,
    np.array([request_counts[-1]] * (DAY // 2)),
])
trend = np.convolve(x, np.ones((DAY,)) / DAY, 'same')
trend = trend[DAY // 2:-(DAY // 2)]

이제 trend에 대해서 time seires forecasting을 진행하고, 예측 값에 seasonal pattern을 적용하면 된다.

경향성 데이터 예측

예측 모델은 매우 간단하게 scikit-learn의 LinearRegressor를 활용했다.

다만 입력 데이터를 단순히 단변량 timeseries로 넣지는 않았고, 1차 및 2차 변화량도 추가했다. 모델 훈련을 위한 데이터셋은 아래와 같이 작성했다.

def ts_to_dataset(X, input_length=DAY, output_length=DAY, test=0):
    assert test >= 0 and test < 1

    window_size = input_length + output_length

    D = X[1:] - X[:-1]
    H = D[1:] - D[:-1]
    X = X[2:]; D = D[1:]

    # PERIOD // 2만큼 제거하고 훈련하는 이유는 더미 데이터로 moving average 값을 얻었기 때문
    indices = np.stack([np.arange(X.shape[0] - window_size - PERIOD // 2)] * window_size) + np.arange(window_size)[..., np.newaxis]
    X = X[indices.T]
    D = D[indices.T]
    H = H[indices.T] # (N, T)

    inputs = np.concatenate([X[:, :input_length], D[:, :input_length], H[:, :input_length]], axis=1) # (N, IN * 3)
    outputs = X[:, -output_length:]

    if test:
        idx = int(X.shape[0] * (1 - test))
        inputs_train = inputs[:idx]
        outputs_train = outputs[:idx]
        inputs_test = inputs[idx:]
        outputs_test = outputs[idx:]
        args = np.arange(inputs_train.shape[0])
        np.random.shuffle(args)
        return inputs_train[args], outputs_train[args], inputs_test, outputs_test
    else:
        args = np.arange(inputs.shape[0])
        np.random.shuffle(args)

        return inputs[args], outputs[args]

input_length가 DAY라는 것은 모델이 하루 치 시계열 데이터를 입력 받아 학습한다는 것이고, output_length가 DAY라는 것은 앞으로 하루 치의 데이터를 예측한다는 것이다.

모델은 아래와 같이 작성하였다.

from sklearn import linear_model

def train_model(X, y, test_X=None, test_y=None):
    assert (test_X is None and test_y is None) or (test_X is not None and test_y is not None)
    do_test = test_X is not None

    reg = linear_model.LinearRegression()
    reg.fit(X, y)

    if do_test:
        y_pred = reg.predict(test_X)
        mse = np.mean((y_pred - test_y) ** 2)
        return reg, mse
    else:
        return reg

그러면 다음과 같이 모델을 훈련할 수 있다. 아래 코드는 test에 대한 고려 없이 모든 데이터를 train 데이터로 활용한다.

# 36시간의 데이터를 보고 이후 12시간의 데이터를 예측
input_length=int(DAY * 1.5); output_length=DAY // 2
train_X, train_y = ts_to_dataset(trend, input_length=input_length, output_length=output_length)
model = train_model(train_X, train_y)

모델이 잘 훈련되었다면 이제 실제 예측을 작성할 수 있다.

predicted_timestamps = np.array([timestamps[-1] + timedelta(seconds=PERIOD * i) for i in range(output_length)])
inputs = trend[-input_length - output_length - 3:]
X, y = ts_to_dataset(inputs, input_length=input_length, output_length=output_length)
y_pred = model.predict(X)[0]
y_pred = y_pred * expand_weekly_pattern(weekly_pattern, predicted_timestamps)

대단할 것 없이 무지성으로 seasonal_decompose를 반복하고, 단순한 LinearRegressor를 활용한 모델은 어떤 결과를 만들어낼까?

테스트 셋을 분리해 학습하고 그 결과를 확인해보았다.

train_X, train_y, test_X, test_y = ts_to_dataset(trend, input_length=input_length, output_length=output_length, test=0.1)
model, mse = train_model(train_X, train_y, test_X, test_y)

plt.plot(timestamps, request_counts)
plt.plot(timestamps, trend)
for i, y in enumerate(model.predict(test_X[::HOUR])):
    o = -(output_length) - len(test_X) + i * HOUR
    t = timestamps[o:o + output_length]
    plt.plot(t, y * C, c='k', linewidth=0.5)
    plt.plot(t, y * C * expand_weekly_pattern(weekly_pattern, t), c='k', linewidth=0.5)

plt.show()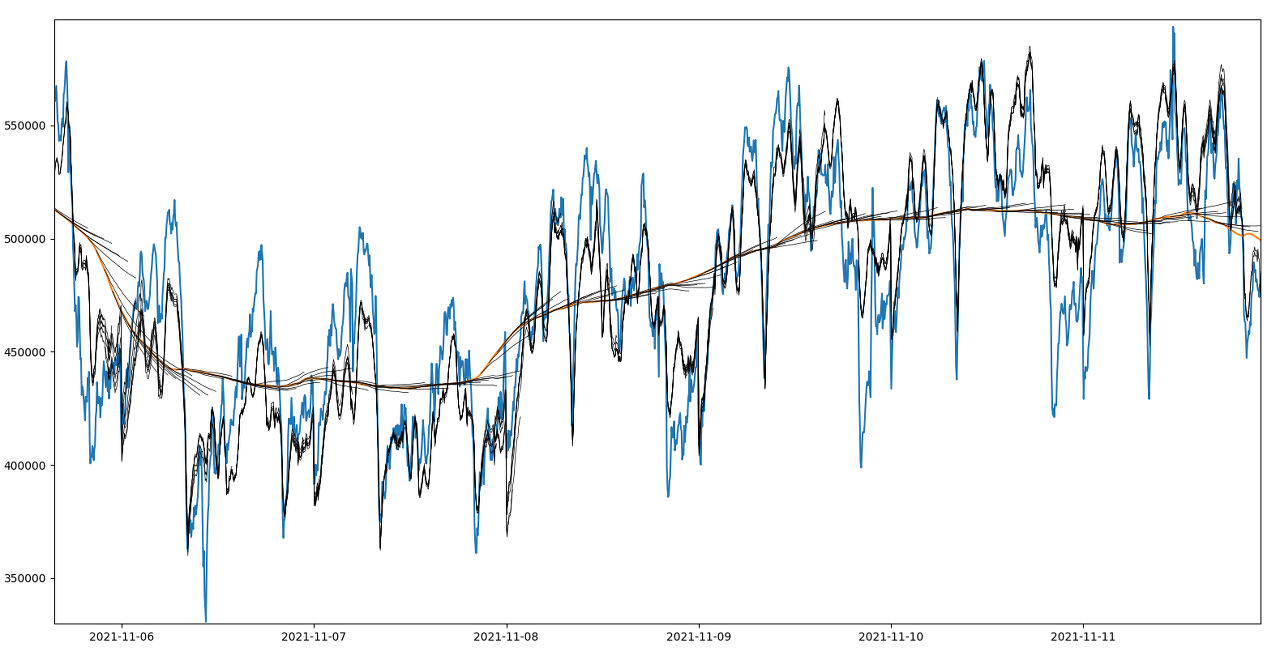

파란색이 실제 데이터, 주황색이 실제 trend 데이터, 검정색이 예측된 trend 데이터와 거기에 seasonal pattern을 곱한 결과이다.

trend 데이터가 가장 가파른 부분을 확대하면 아래와 같다.

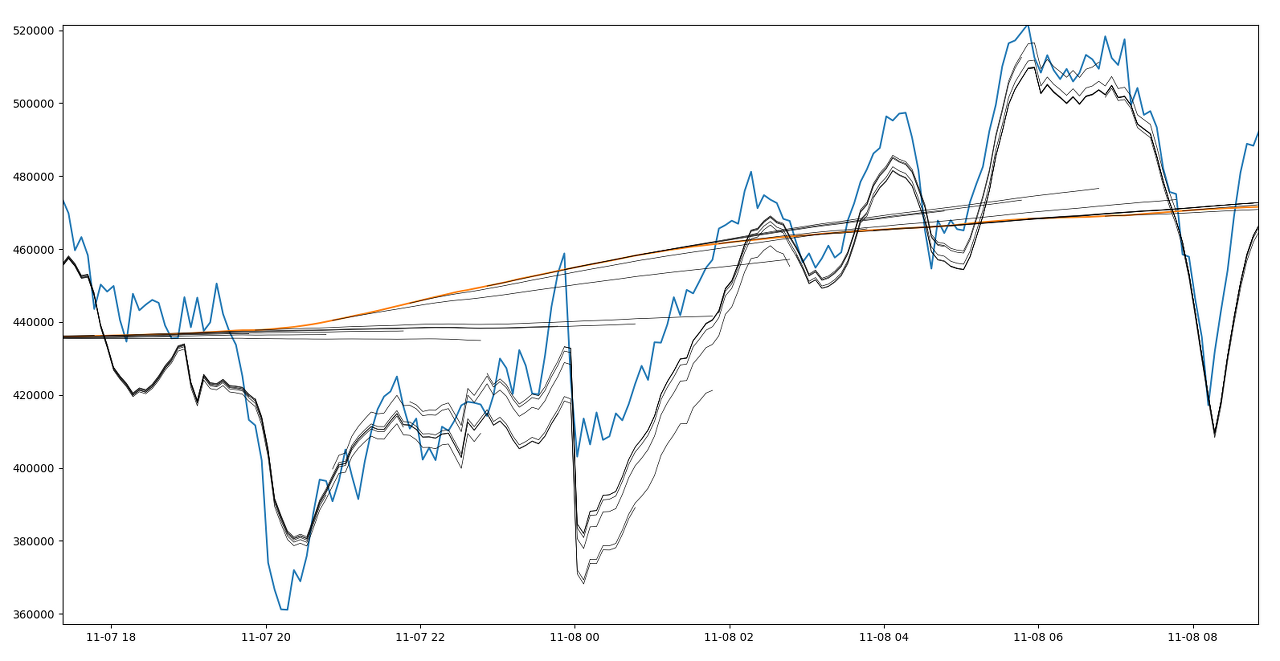
높은 정확도를 원하는 경우 이런 결과가 만족스럽지 못할 수도 있으나, 실무적으로 이 정도의 정확도만 있어도 충분한 경우가 있다. 특히 스케일링의 경우 실제 트래픽을 넉넉히 감당할 수 있도록 진행하기 때문에 대략적인 패턴만 예측할 수 있어도 큰 문제는 없을 것이다.

참고로 API화 했을 때 t3.small 정도만 써도 5초 내지로 걸려서 예측 결과를 실시간으로 리턴하는 것을 확인했다.

---

여담

오늘 어쩌다보니 내가 다니는 회사와 비슷한 BM, 비슷한 백엔드 시스템, 그리고 비슷한 데이터 분포 및 유형을 가진 회사의 MLE와 대화할 일이 있었다.

 

그분도 트래픽은 아니지만 이런 비슷한 time series forecasting을 하고 계셔서 조금 얘기를 나누었다.

 

나온 얘기 중에 하나가, 계절성 패턴에서 벗어나는 비정기적 이상치들을 어떻게 예측하는가였는데, 나는 솔직히 그걸 예측하는 건 쉽지 않다고 생각한다.

아마 딥러닝이라면 이런 것이 가능할 것이다. 평소의 패턴대로 지표가 찍히는데 급증 혹은 급감할 전조가 보이는 경우다. 이런 전조부터 이미 분석된 seasonal pattern에서 벗어난 것이고, 이에 민감하게 반응하여 이상치를 예측하는 가능할 것이다.

 

그러나 우리 회사나 그 분 회사 서비스의 경우 (서비스 구조적으로) 전조 없이 갑작스런 peak가 발생하는 경우가 정말 많다. 이런 것은 이상치에 대한 예측이 아니라 대응이 중요하다고 생각한다. 좀더 고수준의 cold starting이나, anormaly detection쪽으로 고민해보면 좋지 않을까 싶다.