코드는 수없이 테스트당한다. 이것이 정상적으로 작동하는지에 대해서 말이다. 그런데 해당 코드가 "정상"인가에 대한 조건을 세밀히 정의해두지 않는다면 의도치 않은 현상이 발생할 수 있다. 특히나 난수를 활용한 기능들에서 그렇다. 그렇기에 이런 기능들의 결과는 수차례 반복하여 결과를 수집하고 그 분포가 의도한 바와 같은지도 테스트해야 한다.(=이를 "정상 작동"의 조건에 포함시켜 테스트를 진행해야 한다.)
본 포스팅에서는 난수를 활용한 코드를 단순히 작성하면 안됨을 강조하기 위해 시퀀스에서 서브 시퀀스를 랜덤하게 추출하는 여러가지 방법과 그 결과들이 다름을 제시해보려고 한다.
시퀀스의 랜덤 서브 시퀀스 추출하기
리스트든 배열이든, 어떤 시퀀스 데이터를 생각해보자. 길이가 $N$인 아무 시퀀스를 $A$라고 하면 $A={a_i} (i\in[1, N])$이다. $A$의 서브 시퀀스를 얻는 작업은 매우 간단하다. $A$의 서브 시퀀스 $B$를 다음과 같이 정의하자.
$$
B={a_i}\ \ \ (i\in[p, q],\ p,q\text{는 1과 N 사이의 임의의 자연수})
$$
이제 코딩으로 생각해보자. 파이썬은 slice라는 강력한 기능을 지원하므로, 서브 시퀀스를 추출하는 건 아주 쉬운 일이다. 예를 들어 $N$ 길이 리스트가 있을 때 3번째 원소부터 절반 길이까지의 서브 시퀀스를 추출하는 코드는 다음과 같다.
N = 100
A = list(range(N))
B = A[2:N // 2 - 1]랜덤한 길이의 서브 시퀀스를 추출하는 코드는 어떻게 작성할 수 있을까? 방법이 여러가지 있을 수 있겠지만 쉽게 떠오르는 건 다음과 같은 코드일 것이다.
import random
def get_random_sequence(A):
N = len(A)
left = random.randint(0, N)
right = random.randint(0, N)
if left > right: left, right = right, left
B = A[left:right]
return B이 코드는 분명 랜덤한 서브 시퀀스를 리턴한다. 하지만 확률과 통계를 공부한 사람은 조금 더 띵킹을 해볼 필요가 있다.
일반적으로 랜덤의 의미는 $N$분의 1 확률로 여겨진다. 이를 좀 더 고상한 말로 표현하면 uniform하다고 한다. 기초/일반 통계학을 배운 사람들은 균등 분포(uniform distribution)이라는 단어를 배웠을 것이다.
$1$부터 $N$까지 임의의 수를 uniform하게 뽑으면 각각의 수가 뽑힐 확률이 ${1\over N}$이 된다.
그러면 위의 코드는 uniform한 서브 시퀀스를 추출하는 걸까? 적어도 left와 right 인덱스는 uniform하다(random.randint함수는 균등 분포에서 추출한 값을 리턴한다).
하지만 그 서브 시퀀스의 길이는 균등하지 않을 수도 있다. 다음과 같은 코드를 짜보자.
import numpy as np
import matplotlib.pyplot as plt
import random
def get_random_subsequence(A):
N = len(A)
left = random.randint(0, N)
right = random.randint(0, N)
if left > right: left, right = right, left
B = A[left:right]
return B
iter_count = 10 ** 6
A = np.arange(10000)
lengths = [len(get_random_sequence(A)) for _ in range(iter_count)]
plt.hist(lengths, bins=len(set(lengths)) // 100)
plt.show()
뭔가 이상하다. 1,000,000번 반복하여 랜덤 서브 시퀀스를 추출했는데, 길이가 0인 서브 시퀀스가 2만개 가까이 추출되었으며, 길이가 6000인 서브 시퀀스는 7500개 정도 추출되었다. 길이가 9,999인 서브 시퀀스는 매우 조금 추출되었다. 이는 즉, get_random_subsequence 함수는 길이가 짧은 서브 시퀀스를 반환하는 경향이 있다는 것이다.
이는 사소할 수도 있지만, 백엔드에서 이런 기능이 자주 요청될 경우 특정 현상이 일어나도록 하는 원인이 될 수 있다. 만약 그런 현상을 의도하지 않았고, 결과 분포를 테스트하지 않아 이를 인지하지 못했을 경우 바람직하지 않은 상황이 충분히 일어날 수 있다.
왜 이런 일이 일어나는 걸까?
자연수 $\text{left}$와 $\text{right}$에 대해 $$\text{left} \thicksim \text{Uniform}(1,\ N),\ \text{right} \thicksim \text{Uniform}(1,\ N)$$라 하면, 서브 시퀀스의 길이가 $k$일 확률을 다음과 같이 표현한다.
$$
p(|\text{left}-\text{right}|=k)
$$
$x\thicksim \text{Uniform}(1,\ N)$와 같은 표시는 $1$부터 $N$ 사이의 임의의 수들 중 균등하게 아무 수룰 뽑아 $x$로 삼겠다는 의미이다. (쉬운 이해를 위해 연속 분포에 대해서는 논하지 않고, 이산 균등 분포라고 가정한다.)
서브 시퀀스의 길이가 $k$인 경우를 생각하자. $\text{left} + k=\text{right}$이거나 $\text{left}=\text{right} + k$로 두 가지 경우가 있다. 전자의 경우 가능한 경우의 수가 $\text{left}\in[1,N-k+1]$이므로 총 $N-k+1$가지이다. 후자의 경우도 $\text{right}\in[k, N]$이므로 마찬가지이다.
따라서 서브 시퀀스의 길이가 $k$인 경우의 수는 $2(N-k+1)$이고, 그 확률은
$$
p(|\text{left} - \text{right}|=k)={2(N-k+1)-1\over N^2}
$$
가 된다. $2(N-k+1)\over N^2$이 아니라 ${2(N-k+1)-1\over N^2}$인 이유는 두 수가 같은 경우가 중복되기 때문이다.
${2(N-k+1)-1\over N^2}$는 $k$에 대해 선형적이며, $k$가 작을수록 높은 확률을 가진다는 걸 알 수 있다.
따라서 정말 랜덤한 서브 시퀀스를 추출하기를 원한다면 다른 방식으로 추출해야 한다. 다음과 같은 코드는 어떨까?
def get_random_subsequence(A):
N = len(A)
left = random.randint(0, N)
right = random.randint(left, N) # [0, N]에서 뽑지 않고 [left, N]에서 뽑는다.
B = A[left:right]
return B랜덤 서브 시퀀스를 추출하라고 할 때 이런 식으로 구현하는 사람도 정말 많다. left와 right를 swap을 하지 않아도 되기에 훨씬 더 간편하고 쉬운 코드라고 생각될 수도 있다. 이 함수도 마찬가지로 결과 분포를 살펴보자.

아까의 함수보다 더 괴랄한 모양이 나왔다. 매우 짧은 길이의 서브 시퀀스가 훨씬 더 많이 추출된다. 이 코드도 확률을 구해보자.
자연수 $\text{left}$와 $\text{right}$에 대해 $$\text{left} \thicksim \text{Uniform}(1,\ N),\ \text{right} \thicksim \text{Uniform}(\text{left},\ N)$$라 하면, 서브 시퀀스의 길이가 $k$일 확률을 다음과 같이 표현한다.
$$
p(\text{right}-\text{left}=k)
$$
서브 시퀀스의 길이가 $k$이려면 $\text{left}$가 될 수 있는 경우의 수는 아까와 동일하게 $N-k+1$개이다. 그러나 $\text{right}\in[\text{left}, N]$는 $\text{right}=\text{left}+k$인 경우 하나뿐이다.
따라서 ${1\over N}$의 확률로 어떤 $\text{left}$값이 정해지고, 이후 ${1\over N-\text{left}+1}$의 확률로 $\text{right}$값이 정해진다.
그러면 확률을 다음과 같이 표현할 수 있다.
$$
p(\text{right}-\text{left}=k)=\sum_{\text{left}=1}^{N-k+1}{1\over N}\times{1\over N-\text{left} + 1}
$$
정리하기 힘든 식이다. 본문의 메인 주제가 아니므로 굳이 정리하지 않겠다. 대충 포물선 처럼 생긴 분포가 아닐까... 생각한다.
아무튼 중요한 것은, uniform한 분포로부터 임의의 인덱스를 추출하는 것이 의도치 않게 균등하지 않은 시퀀스를 리턴할 수 있다는 부분이다.
다시 말하지만, 이런 의도되지 않은 분포는 서비스 도중 의도되지 않은 현상을 일으킬 가능성이 있다.
그러면 정말로 균등한 서브 시퀀스를 리턴하는 함수는 어떻게 작성하는 걸까? 다음과 같이 작성해야 한다.
알고리즘대로의 구현 방식은 다음과 같다.
def get_random_subsequence(A):
N = len(A)
length_of_subsequence = random.randint(0, N)
left = random.randint(0, N - length_of_subsequence)
right = left + length_of_subsequence
B = A[left:right]
return B이런 식으로 구현해야 서브 시퀀스의 길이가 uniform한 분포로부터 샘플링될 수 있다. 너무 당연하게도 길이 자체가 균등 분포로부터 추출되기 때문이다.
($$\text{length}\thicksim\text{Uniform}(1, N),\ p(\text{length}=k)={1\over N}$$)

그러면 세 번째 방식으로 서브 시퀀스를 추출하는 게 옳은 일일까? 확신하기 어렵다.
세 번째 방식은 서브 시퀀스의 길이가 균등하게 추출되도록 하는 방식이다. 길이도 균등하게 샘플링되면서 모든 요소가 균등하게 추출되길 원할 수도 있다. 예를 들어 원본 시퀀스의 0번 인덱스 요소가 $k$번 추출되었다면 다른 $i$번째 요소도 $k$번에 가깝게 추출되는 것이다.
그러나 세 번째 방법은 척 봐도 이를 만족할 것 같지가 않다. 아마 중간의 요소들 위주로 샘플링될 것이다. 아래와 같은 코드로 확인해보자.
iter_count = 10 ** 3
A = np.arange(1000)
subsquences = [get_random_subsequence(A) for _ in range(iter_count)]
elements = np.concatenate(subsquences)
counts = np.zeros((1000,))
for a in A:
counts[a] += (elements == a).sum()
plt.bar(A, counts)
plt.show()(연산이 무거울 듯해 반복수와 시퀀스의 길이를 줄였다.)
위 코드의 결과는 아래와 같다.
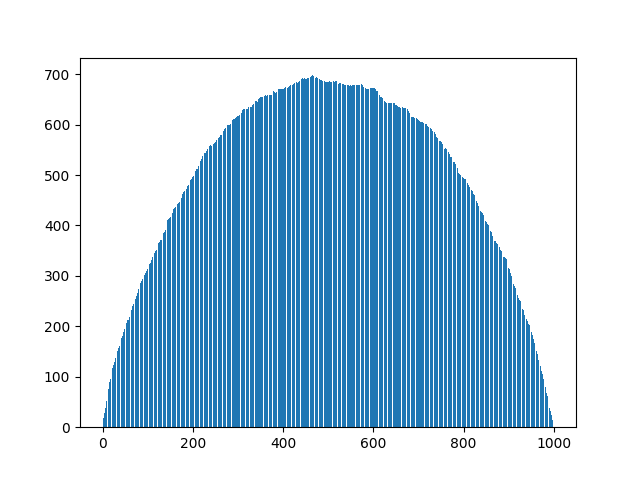
이처럼 길이가 균등하게 추출되어도 요소별 추출 빈도는 다를 수가 있다. 길이도 균등하며 요소별 추출빈도도 균등한 샘플링 방법이 있을까? 있을지 없을지 생각해보진 않았다만 골치가 아플 것 같다.
결론
본 포스팅을 통해 난수 생성을 어떻게 활용하냐에 따라 결과가 크게 달라짐을 확인하였다. 난수 생성 함수는 대부분 균등 분포인데, 균등 분포로부터 추출된 변수들의 조합은 균등 분포가 아닐 가능성이 높다. 그러므로 난수를 생성하는 코드를 작성할 때에는 반드시 의도하는 결과를 생각해두고, 이에 맞게 함수를 설계한 뒤, 샘플링하여 의도한 결과가 나오는지 테스트할 필요가 있다.
본문에서는 '서브 시퀀스'라는 틀에 갇혀있는데, 사실 여러가지 다른 샘플링 방법을 쓰면 발생할 법한 문제들의 해결이 쉽다. 다만 필자가 말하고 싶은 것은, 개발자가 아무 생각 없이 작성한 코드로 인해 고객에게 전달되는 가치가 변형될 수 있다는 것이다. (일어나기 매우매우매우 힘든 일이지만) 아무렇게나 작성한 코드가 만약 고객 추첨 코드였고 균등하지 못한 결과로 인해 특정 고객들에게만 특혜가 갔다면? 고객과 서비스 제공자 둘 다에게 썩 좋은 상황은 아닐 것이다. 그러니 모든 기능이 않그렇겠냐마는, 난수가 활용되는 코드에는 테스트에 조금 더 신경을 써보는 것이 좋겠다.
+이런 부분의 코드를 작성하는 데 있어 통계적인 인사이트가 조금 도움되지 않을까 생각한다.
'개발 > 파이썬' 카테고리의 다른 글
| 파이썬의 메서드 결정 순서(Method Resolution Order)와 프로토콜에 의한 일관성 유지 (0) | 2022.12.02 |
|---|---|
| 파이썬의 루프를 더 빠르게 하는 법? (0) | 2022.11.15 |
| 모션캡쳐 파이썬 구현 (0) | 2022.07.31 |
| Python 네임스페이스에 대한 이해 (0) | 2022.07.09 |
| $D^{-1/2}$는 어떤 방법으로 구해야 할까? np.ndarray와 np.matrix의 차이 (0) | 2022.07.09 |
